实际项目中的红黑树与跳表
引言
日常开发过程中,像大量文本中查找相似文本,缓存数据这些功能,我们并不是直接利用语言原生支持的数据结构来实现。这些专门的应用领域,工程师们会有专门优化的解决方案。例如flann进行相似文本查询,redis进行kv字段缓存。那么这些专门的解决方案,他们的基本的数据结构是什么呢?
红黑树
https://blog.csdn.net/weewqrer/article/details/51866488
用途
C++中的set,map,multimap,multiset底层结构均是红黑树
红黑树严格来说是一种更高效的二叉查找树,它比BST(二叉查找树)和AVL(平衡二叉查找树)更加高效,能够将插入和删除操作的时间复杂度控制在O(log n), 因为高效,被应用在库容器的底层,如STL::map,正是由于高效,因此也多了很多的规则。红黑树的规则一共有五条:
- 节点必须是红色或者是黑色;
- 根节点是黑色;
- 所有叶子节点都是黑色(叶子节点为NULL);
- 任何一个节点和它的父节点不能同时为红色;
- 从根节点到任何一个叶子节点所经过的黑色的节点的数目必须是相同的。
红黑树 VS AVL树
红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。对于查找、插入、删除、最大、最小等动态操作的时间复杂度为\(O(logn)\).常见的用途有以下几种:
- STL(标准模板库)中在set map是基于红黑树实现的。
- Java中在TreeMap使用的也是红黑树。
- epoll在内核中的实现,用红黑树管理事件块。
- linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
常见的平衡树有红黑树和AVL平衡树,为什么STL和linux都使用红黑树作为平衡树的实现?大概有以下几个原因:
从实现细节上来讲,如果插入一个结点引起了树的不平衡,AVL树和红黑树都最多需要2次旋转操作,即两者都是O(1);但是在删除node引起树的不平衡时,最坏情况下,AVL需要维护从被删node到root这条路径上所有node的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度
从两种平衡树对平衡的要求来讲,AVL的结构相较RB-Tree来说更为平衡,在插入和删除node更容易引起Tree的unbalance,因此在大量数据需要插入或者删除时,AVL需要rebalance的频率会更高。因此,RB-Tree在需要大量插入和删除node的场景下,效率更高。自然,由于AVL高度平衡,因此AVL的search效率更高。
总体来说,RB-tree的统计性能是高于AVL的
相关应用
近似近邻算法在大型应用中是解决搜索的关键技术。而近似近邻算法的研究中,一部分是基于树结构实现的,一部分是基于hash算法。今FLANN是一个开源库,opencv中已经集成了该module.
FLANN概述
首先阐述了近似结果查询的重要性,通过实验结果分析了最有效的近似nn算法中,随机KD森林是最有效的,另外提出了一个新的方法:优先查找k-means树,尤其是针对视觉任务中常用的二进制特征,提出了多层聚类树。为了应用于大数据环境下,还有分布式环境下nn查找框架。
相关名词定义
- KNN(K-nearest neighbor search):说白了,就是从数据集合了找K个最接近的
- RNN(radius nearest neighbor search):就是返回一定半径范围内的所有数据。当然这个半径有很多不同的定义。
参考文献
SkipList
skiplist本质上也是一种查找结构,用于解决算法中的查找问题(Searching),即根据给定的key,快速查到它所在的位置(或者对应的value)。
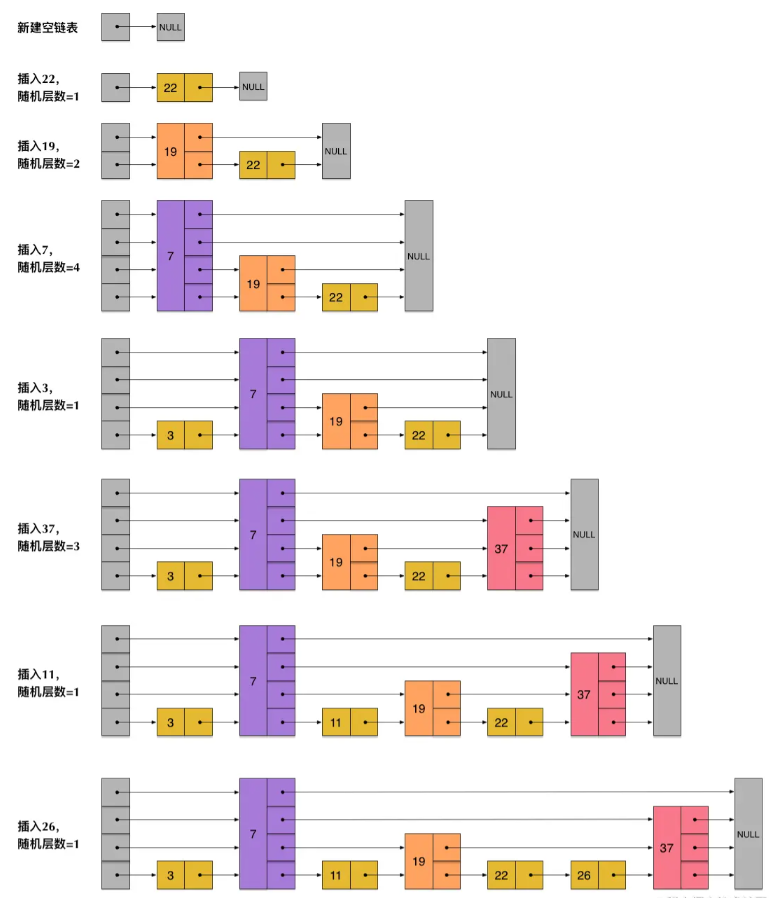
skiplist与平衡树、哈希表的比较
skiplist和各种平衡树(如AVL、红黑树等)的元素是有序排列的,而哈希表不是有序的。因此,在哈希表上只能做单个key的查找,不适宜做范围查找。所谓范围查找,指的是查找那些大小在指定的两个值之间的所有节点。
范围查找的时候,平衡树比skiplist操作要复杂。在平衡树上,我们找到指定范围的小值之后,还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造,这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单,只需要在找到小值之后,对第1层链表进行若干步的遍历就可以实现。
平衡树的插入和删除操作可能引发子树的调整,逻辑复杂,而skiplist的插入和删除只需要修改相邻节点的指针,操作简单又快速。
从内存占用上来说,skiplist比平衡树更灵活一些。一般来说,平衡树每个节点包含2个指针(分别指向左右子树),而skiplist每个节点包含的指针数目平均为1/(1-p),具体取决于参数p的大小。如果像Redis里的实现一样,取p=1/4,那么平均每个节点包含1.33个指针,比平衡树更有优势。
查找单个key,skiplist和平衡树的时间复杂度都为O(log n),大体相当;而哈希表在保持较低的哈希值冲突概率的前提下,查找时间复杂度接近O(1),性能更高一些。所以我们平常使用的各种Map或dictionary结构,大都是基于哈希表实现的。
从算法实现难度上来比较,skiplist比平衡树要简单得多。